***Please note that it will be most advantageous if you have a firm understanding of Colour before you begin this project. Intro to Colour Project
***Please, please, note that the following unity is meant as the backdrop to a lecture.
OK, let’s listen to some Tycho, The science of patterns while we talk about patterns
As we listen I would like you to think not only of Pattern but of repetition and rhythm as well.
Curriculum objectives:
- Big idea: Pattern is a huge topic that can be used to talk about the history of humanity, the spread of disease, Math and a whole lot more,,, really almost everything we know can be talked about in relationship to patterns.
- In this unit, we will explore the patterns as structure. Talk about how artists use pattern. Use patterns as a means to deepen our understanding of colour theory.
- Students will design and produce patterns based on Ideas and colour schemes.
In this Page you will find the following sections:
What is a pattern?
Patterns from around the world
Types of Patterns
Articles about Patterns and the world we live in
Task
Marking criteria
___________________________________

Image source http://whitney.org/Exhibitions/TestPattern
What is a pattern?
Pattern is the underlying structure that organises surfaces or structures in a consistent, regular manner. Patterns can be described as a repeating unit of shape or form, but it can also be thought of as the “skeleton” that organises the parts of a composition.
Pattern exists in nature as well as in designed objects; it is useful to look at the parallels. A Harvard biologist named Peter S. Stevens has published a book entitled “Patterns in Nature” in which he claims that there are only a finite number of ways that patterns can be structured. He starts with the idea of a grid as the foundation for any structure or image. He presents a set of ways in which the points of a grid can be connected. These modes of connection become classes of pattern, which he claims can be seen in any situation, in nature and in made images, and from the microscopic to the cosmic scale.
Image source www.spoonflower.com
The modes he describes include the following which are described here in terms of examples from nature. However, each of these modes can also be seen in examples of designed objects and works of art:
(text source http://char.txa.cornell.edu/language/element/pattern/pattern.htm)

Image source www.inspirememandalas.com
Humans are natural pattern recognizers. Whether, as in prehistoric times, we were recognizing danger in a telltale rustle of the bushes or skimming a page of letters and numbers today, we use patterns to derive meaning without having to do a more detailed inspection.
Futurist and entrepreneur Ray Kurzweil considers pattern recognition so important that in his recent book, How to Create A Mind, he argued that pattern recognition and intelligence are essentially the same thing. Expertise, in essence, is the familiarity of patterns of a specific field.
Image source http://www.wallpaperhd.pk/
Today, machines are learning to recognize patterns as well. Marketers analyze patterns to target their messages and IBM’s Watson can detect patterns embedded in millions of documents in fields such as medicine. However, there’s a problem with patterns. Just as they can uncover hidden meaning, they can also make us see things that aren’t really there. (Greg Satell http://www.forbes.com/sites/gregsatell/2015/05/01/the-science-of-patterns/#10ef6c565361)
Patterns from around the world
Let’s take a look at some patterns found around our world. Click on the image below for a slide show.
The History of Patterns:
- Patterns are as old as humanity. We can see Patterns on early clay shards, cave paintings, early textiles and basketry.
- Can we see history as a pattern?
- Could it be said that the history of humanity is the history discovery the patterns around us how we have incorporating them into our lives?
Types of patterns:
Nature provides examples of many kinds of pattern, including symmetries, trees and other structures with a fractal dimension, spirals, meanders, waves, foams, tilings, cracks and stripes.[2]
Symmetry
Image source https://sylvaindeville.net/2015/03/10/snowflakes-engineered/
Symmetry is widespread in living things. Animals that move usually have bilateral or mirror symmetry as this favours movement.[3] Plants often have radial or rotational symmetry, as do many flowers, as well as animals which are largely static as adults, such as sea anemones. Fivefold symmetry is found in the echinoderms, including starfish, sea urchins, and sea lilies.[4]
Among non-living things, snowflakes have striking sixfold symmetry: each flake is unique, its structure recording the varying conditions during its crystallisation similarly on each of its six arms.[5] Crystals have a highly specific set of possible crystal symmetries; they can be cubic or octahedral, but cannot have fivefold symmetry (unlike quasicrystals).[6] (Text source https://en.wikipedia.org/wiki/Pattern)

Image source http://fineartamerica.com/featured/ghosts-of-symmetry-joel-kahn.html
Symmetry in Art images
(*An excellent article! The Simplest Diagram of the 17 Symmetry Types, Ever)
Spirals
Image source axesmundi.blogspot.com
Spiral patterns are found in the body plans of animals including molluscs such as the nautilus, and in the phyllotaxis of many plants, both of leaves spiralling around stems, and in the multiple spirals found in flowerheads such as the sunflower and fruit structures like the pineapple.[7] (Text source https://en.wikipedia.org/wiki/Pattern)
Image source http://art-now-and-then.blogspot.ca/2016/01/remedios-varo.html
(If you like the painting above by Remedios Varo CLICK HERE to see more of her work)
Spirals in Art
Chaos, flow, meanders
Can you guess what the image below is?
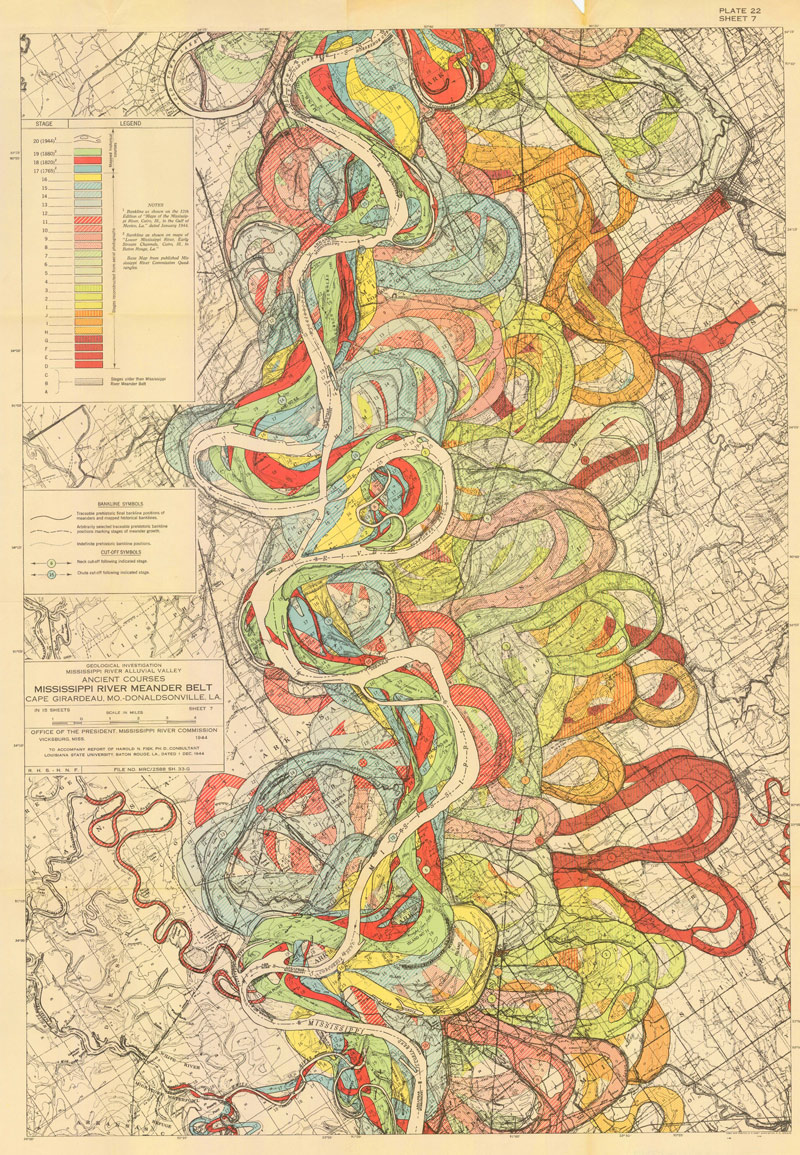
Image source www.cardus.ca
It is a pictorial history of all the different routes the Mississippi has taken over thousands of years.
Chaos theory predicts that while the laws of physics are deterministic, events and patterns in nature never exactly repeat because extremely small differences in starting conditions can lead to widely differing outcomes.[8] Many natural patterns are shaped by this apparent randomness, including vortex streets[9] and other effects of turbulent flow such as meanders in rivers.[10] (Text source https://en.wikipedia.org/wiki/Pattern)
Image source Wikipedia A double rod pendulumanimation showing chaotic behavior. Starting the pendulum from a slightly different initial condition would result in a completely different trajectory. The double rod pendulum is one of the simplest dynamical systems that has chaotic solutions
There are even patterns in static or white noise Click here
Spots, stripes

Image source nationalaquarium.wordpress.com
Main article: Pattern formationAlan Turing,[16] and later the mathematical biologist James D. Murray[17] and other scientists, described a mechanism that spontaneously creates spotted or striped patterns, for example in the skin of mammals or the plumage of birds: a reaction-diffusion system involving two counter-acting chemical mechanisms, one that activates and one that inhibits a development, such as of dark pigment in the skin.[18] These spatiotemporal patterns slowly drift, the animals’ appearance changing imperceptibly as Turing predicted. (Text source https://en.wikipedia.org/wiki/Pattern)
Here is another interesting non-equilibrium thermodynamics a Belousov–Zhabotinsky reaction. Take a look.
A Belousov–Zhabotinsky reaction’, orBZ reaction, is one of a class of reactions that serve as a classical example of non-equilibrium thermodynamics, resulting in the establishment of a nonlinearchemical oscillator. The only common element in these oscillators is the inclusion of bromine and an acid. The reactions are important to theoretical chemistry in that they show that chemical reactions do not have to be dominated by equilibrium thermodynamic
behavior
. These reactions are far from equilibrium and remain so for a significant length of time and evolve chaotically. In this sense, they provide an interesting chemical model of nonequilibrium biological phenomena, and the mathematical models of the BZ reactions themselves are of theoretical interest and simulations.
(text source https://en.wikipedia.org/wiki/Belousov%E2%80%93Zhabotinsky_reaction#cite_note-1)
Artist Michael Carson
Image source http://artcontrarian.blogspot.ca/2011/03/dialing-it-back.html
Art and architecture
Image source wikioedia
Elaborate ceramic tiles at Topkapi Palace
Tilings
The Art of Elegant Tiling
Mathematics and art have many points of contact, but none is more beautiful than the concept of symmetry. The mathematician’s approach to symmetry is a little too rigid for most forms of visual art, but it can be readily applied to any art form that features repetitive patterns. Wallpaper, fabrics and tiles are familiar examples, and all of them can rise to great artistic heights. Tiles and wallpaper designed by 19th-century British artist William Morris are displayed in London’s Victoria and Albert Museum. The Edo-Tokyo Museum possesses some absolutely outstanding examples of patterned kimonos, and the Alhambra palace in Granada, Spain, is renowned worldwide for its intricate tiled patterns.
Although the basic mathematics of symmetry and tilings was worked out long ago, new discoveries continue to be made, often by artists. Rosemary Grazebrook, a contemporary British artist, has invented a remarkably simple tiling system that is eminently practical and different enough from the usual rectangular tiles to be interesting. It is also ingenious and, in the right hands, beautiful.
(*To read more of Ian Stewart’s article The Art of Elegant Tiling CLICK HERE)
Tessellation and Tile
In visual art, pattern consists in regularity which in some way “organises surfaces or structures in a consistent, regular manner.” At its simplest, a pattern in art may be a geometric or other repeating shape in a painting, drawing, tapestry, ceramic tiling or carpet, but a pattern need not necessarily repeat exactly as long as it provides some form or organising “skeleton” in the artwork.[19] In mathematics, a tessellation is the tiling of a plane using one or more geometric shapes (which mathematicians call tiles), with no overlaps and no gaps.[20]Text source https://en.wikipedia.org/wiki/Pattern)
Have you seen the tessellations of MC Escher?

Image source http://britton.disted.camosun.bc.ca/ By Escher

Image source http://britton.disted.camosun.bc.ca/
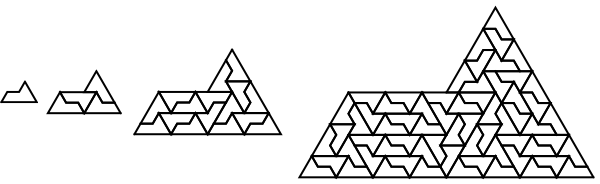
Image source http://mathstat.slu.edu/escher/index.php/Aperiodic_Tessellations
To draw a substitution tiling by hand, begin with a large version of the tile, subdivide it into smaller copies of itself, and then continue subdividing each smaller copy until the desired level of detail is reached:
Image source http://mathstat.slu.edu/escher/index.php/Aperiodic_Tessellations
In the Extension Theorem, the tile (or tiles) are required to cover ‘larger and larger’ patches of the plane. This is intended to mean that the tile can cover as large a patch as desired, or that there is no limit to the size of a patch covered by the tile. One might ask if there is some patch size that is always large enough. As an example for thought, the tile shown below is a hexagon with one flat side, two spiked sides, and three dents. The spikes fit into the dents, and for a while this tile can build a tessellation, but eventually the dents outnumber the spikes and one gets stuck – Amman’s dented hexagon cannot tile the plane, even though it can tile a fairly large patch: (*To read more from this sitehttp://mathstat.slu.edu Please CLICK HERE)
How to Draw Islamic Geometric Patterns
Science and mathematics
Image source wikapedia
Fractal model of a fern illustrating self-similarity
Mathematics is sometimes called the “Science of Pattern”, in the sense of rules that can be applied wherever needed.[23] For example, any sequence of numbers that may be modeled by a mathematical function can be considered a pattern. Mathematics can be taught as a collection of patterns.[24] (Text source https://en.wikipedia.org/wiki/Pattern)
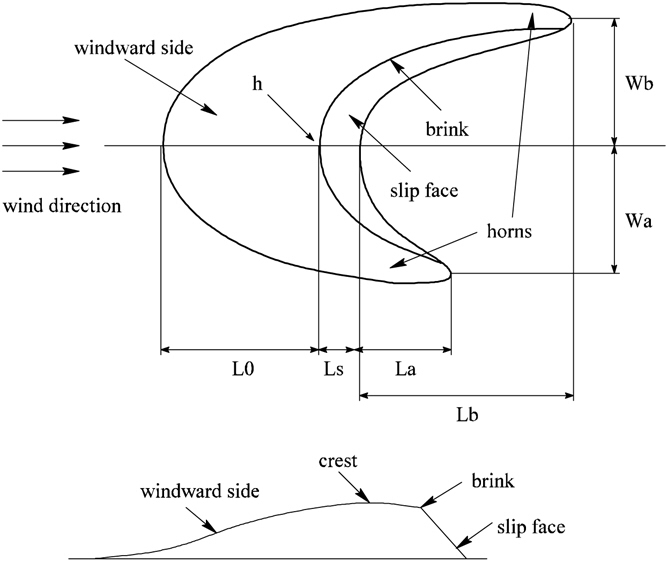
Waves and Dunes

Image source http://giphy.com/
I have to admit that my fascination and captivation with beaches, the place where liquids and solids meet. Ocean wave, the result of wind and the moon’s gravitational pull on the earth, and the Dunes the result of the winds.

Image source http://giphy.com/
Yet,
Sand dunes are ubiquitous, sometimes problematic features of deserts and coastlines. Their undulations call to mind ripples on water, but dunes and water waves differ in crucial ways. In particular, whereas “traveling” water waves are largely illusory, a product of motion that is essentially up and down, the advance of sand dunes really does involve material transport: Individual grains of sand are blown by the wind along nearly horizontal trajectories, as anyone whose face has been sandblasted at the beach on a breezy day will know. Errant dunes have been known to block roads and overrun buildings.
Image source http://www.whydomath.org/Reading_Room_Material/siamnews/sn11_2007.html.
Figure 1. Anatomy of a dune. Forces exerted by wind, gravity, and friction determine the
shape of a barchan. Figure courtesy of Hans Herrmann.
(*For more information Please see Barry A. Cipra’s article on Dune Dynamics- CLICK HERE)
Did you know that waves don’t actually travel from great distances to the beach… no, its more about a transference of energy through water then the movement of water from place to place.

Image source http://www.silvasurflessons.com/what-are-waves/

Artist Franci Bacon, Sand Dune. Image source http://www.tate.org.uk/

Close
Katsushika Hokusai, ‘The Great Wave off Kanagawa’ Image source http://www.vam.ac.uk
Sign waves
This tool will let you HEAR different Frequencies. Click here to go to an online Tone generator.
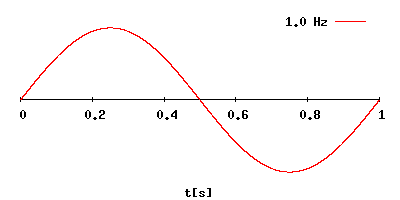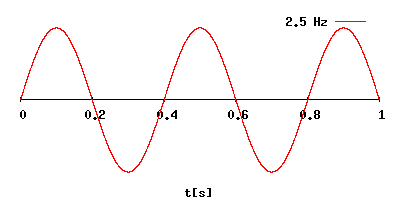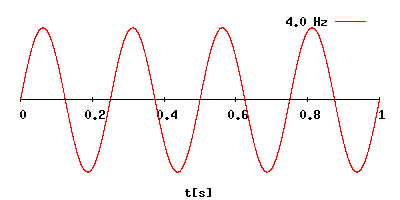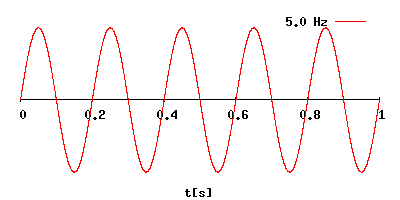
Image source https://en.wikipedia.org/wiki/Hertz
Virtual Oscilloscope
This tool will let you SEE different Frequencies. Click here to go to a Virtual Oscilloscope
Spectrum Analyzer
This audio spectrum analyser (a device for analysing a system of oscillations, especially sound, into its separate components) enables you to SEE the frequencies present in audio recordings which you can HEAR at the same time.
Click here to go to an online audio spectrum analyser
The spectrum analyser above gives us a graph of all the frequencies that are present in a sound recording at a given time. The resulting graph is known as a spectrogram. The darker areas are those where the frequencies have very low intensities, and the orange and yellow areas represent frequencies that have high intensities in the sound. You can toggle between a linear or logarithmic frequency scale by ticking or unticking the logarithmic frequency checkbox.
In many ways, this demo is similar to the Virtual Oscilloscope demo, but there is a crucial and very important difference. In the oscilloscope demo, the plot shows the displacement of an audio signal versus the time, which is called the time-domain signal. This demo shows the signal represented in a different way: the frequency domain. The frequency spectrum is generated by applying a Fourier transform to the time-domain signal.(Text source https://academo.org/demos/spectrum-analyzer/)
Is there a pattern to a bird’s song?
(*For anyone interested in Music and the frequencies of different notes click HERE)
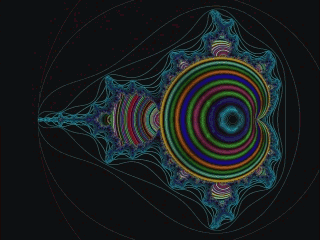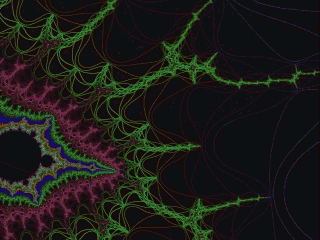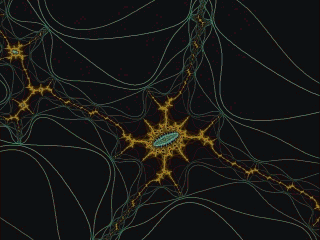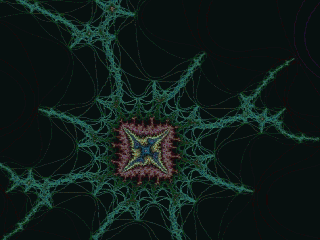
Image source https://upload.wikimedia.org/wikipedia/commons/a/a4/Mandelbrot_sequence_new.gif
Fractals
Some mathematical rule-patterns can be visualized, and among these are those that explain patterns in nature including the mathematics of symmetry, waves, meanders, and fractals. Fractals are mathematical patterns that are scale invariant. This means that the shape of the pattern does not depend on how closely you look at it. Self-similarity is found in fractals. Examples of natural fractals are coast lines and tree shapes, which repeat their shape regardless of what magnification you view at. While self-similar patterns can appear indefinitely complex, the rules needed to describe or produce their formation can be simple (e.g. Lindenmayer systemsdescribing tree shapes).[25]
In pattern theory, devised by Ulf Grenander, mathematicians attempt to describe the world in terms of patterns. The goal is to lay out the world in a more computationally friendly manner.[26]
In the broadest sense, any regularity that can be explained by a scientific theory is a pattern. As in mathematics, science can be taught as a set of patterns.[27] (Text source https://en.wikipedia.org/wiki/Pattern)
(If you want to play with an online fractal generator CLICK HERE)
Computer science
In computer science, a software design pattern, in the sense of a template, is a general solution to a problem in programming. A design pattern provides a reusable architectural outline that may speed the development of many computer programs.[28]
(Text source https://en.wikipedia.org/wiki/Pattern)
Anther aspect of patterns in Computers science is that advent of Binary, Early counting devices and Memory storage devices. Here is an interesting article:
The History of Early Computing Machines, from Ancient Times to 1981

Image source blog.joehuffman.org
Articles about Patterns and the world we live in:
Pattern Recognition and Gene Expression
Pattern Recognition: A Key to Success in Doing Anything Well
Task:
I would like you to think about an area of life that captivates you. Then develop pattern paintings that speak to that area in the way the colour and patterns are designed.
Please use the following colour theories:
- Intermediate or Tertiary
- Secondary
- Complimentary
- Split Complimentary
- Double split complementary
- Analogous (Warm or cool)
- Monochromatic
*The style or look of that patterns is up to you. After seeing all the images above I am hoping you have some ideas!!!
**Please note that some of the images are not really of patterns although they have patterns in them, and in this project, I am really liking for you to develop patterns.
Marking criteria
As discussed in class your painting will be marked on:
- Completion or all 6
- Having an Idea based in content for each patern- content can me anything as long as you define it!
Having 8 different colour theories - No smaller than 3×3″
- No bigger that 6×6″
- Complexity
- Application of paint